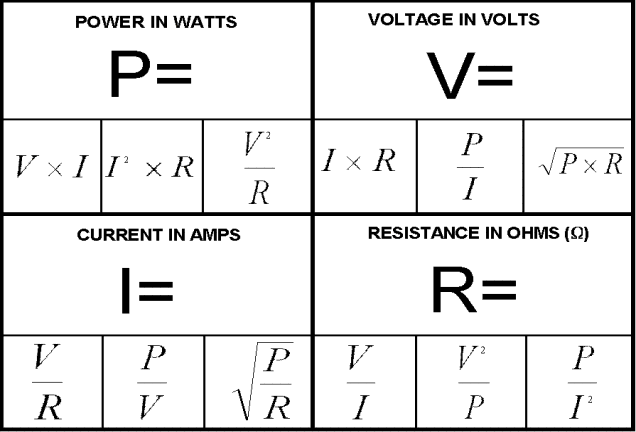In a previous article we looked at the power formula, and discussed the relationship between power, voltage and current. Having looked at the power formula, there is now only one more formula needed to help solve just about every electrical calculation, this is the dreaded Ohms law. We wont get involved with deriving the formula, but take a minute to read the following illustration:

When you turn the tap on connected to a garden hose without a nozzle, you will see water flowing out the other end. The flow of water through the hose is similar to electric current flow – electric current is the flow of electrons through a wire.
If you now put your thumb on the end of the hose and try to block the water flow, the water pressure you feel is like voltage. Voltage is the pressure which pushes the electrons through the wire. What is interesting is that if your thumb completely blocks the water flow, there is still water pressure (voltage). Having a nozzle on the end of the hose and stopping the water flow is like having a wall power socket with nothing plugged in – there is no water/current flow, but the pressure/voltage is still there. The point to note is that voltage is present, even if there is no current flowing. Another example of this is a car battery – it always has 12 volts available to any wire connected to it, no matter what the current drawn.
Back to the garden hose, if you now move your thumb around on the end of the hose, you can vary the amount of water which comes out. That is, as you vary the resistance to the water, you vary the flow. This is same in an electrical circuit – vary the resistance and the current flow changes accordingly. Let’s define electrical resistance as “that which resists, blocks, impedes or restricts current flowing through a circuit”. Examples of a resistance in a circuit are a light bulb or an electrical appliance.
If the voltage (water pressure) remains the same, the current flow will depend on the resistance. The greater the resistance, the less the current flow. Conversely, the less the resistance, the greater the current flow. This is like the more you block the end of the hose the more the water flow decreases, reducing the resistance increases the water flow.
If the resistance remains the same, the current flow can be increased or decreased by increasing or decreasing the voltage (water pressure).

In 1827, a German named Georg Simon Ohm published a book describing the relationship between voltage, current flow and resistance. This relationship is now known as Ohms Law. Ohms law states that current flow is directly proportional to voltage, and inversely proportional to resistance.
Mathematically, it looks like this:
Current = Voltage/Resistance
The symbols and units of measurement for voltage and current are the same as for the power formula. Note the standard terms for resistance.
| Name | Symbol | Units of Measurement |
|---|---|---|
| Current | I | amperes or amps (A) |
| Voltage | V | volts (V) |
| Resistance | R | ohms (Ω) |
Therefore, we can write this formula quickly as:
I = V/R
A popular way to remember this formula and its derivatives is by the triangle shown here. Whatever characteristic you are looking for, place your finger to cover that, and the formula you need remains.
Example 1: To find the voltage of a circuit when you know the resistance and the current, place a finger to cover the “V”, and the formula is I x R.
Example 2: To find the current in a circuit when you know the voltage and resistance, place a finger to cover the “I”, and the formula is V/R
Example 3: To find the resistance of a circuit when you know the voltage and current, place a finger to cover the “R”, and the formula is V/I
In other words, the formula in its three possible forms is:
V = I x R I = V/R R = V/I
Using these formulas and the following circuit, the relationship between resistance and current can be seen, given that the voltage remains the same.
Example 1: Given that the voltage is 220 Volts, and the resistance is 110 ohms(Ω), we can  calculate the current using the formula:
calculate the current using the formula:
I = V/R = 220/110 = 2 Amps
Example 2: Same voltage (220 Volts), but now the resistance is only 2Ω.
I = V/R = 220/2 = 110 Amps
That is, the greater the resistance, the less the current allowed to flow. Also the less the resistance, the greater the current allowed to flow.
Using the water analogy again may be useful. If you had a large diameter water pipe, then a lot of water (current) could flow through it because the “resistance” is low (no blockages). If there is a blockage in the pipe (resistance), then the (current) flow is reduced. The greater the blockage (the higher resistance), the less the (current) flow.
This principle is illustrated in the examples above. In example 1, a resistance of 110Ω allowed only 2 amps to flow through the circuit. In example 2, a small resistance (2Ω) allowed a large current of 110 amps to flow through the circuit.
Resistance is anything that resists current flowing through a circuit. A light bulb is a resistance, as is an iron, a food processor, or a stove. In electronics, there are little components called resistors, which are made to be a fixed known value. Even just plain cable has some resistance, in fact, the reason to have thick cables is to reduce the resistance and allow more current to flow through it (like a fire hose is larger than a garden hose – so more water can flow through it).
P.S.: we have just covered the basic principles of Ohms Law, but shhh, don’t tell anyone.
If you find the maths confusing, try the simple Ohm’s law calculator.
Series or Parallel
Often you don’t know what the resistance in a circuit is, nor do you need to know. However these formulas are still very useful, but mainly for what is derived from them, rather than for their immediate calculation. This is a long-winded way of saying, “please accept that the following concepts are derived from the above formula, without us having to waste time and effort proving it”.
Concept 1:
Consider this circuit of six light bulbs. Because they are connected one after the other, they are said to be connected in series.
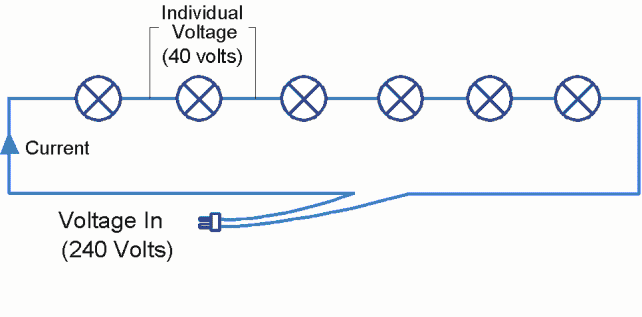 What is interesting is what happens with the voltage, current and resistance.
What is interesting is what happens with the voltage, current and resistance.
Voltage: The “voltage in” is the sum of the voltages across all the individual lights. In this example, the individual voltage across each light is 40 volts, so the total voltage is 240 volts.
Current: The current through each individual light is the same as the current throughout the whole circuit. If the current going to the circuit is 1 amp, then the current through each individual light is also 1 amp.
Resistance: The total resistance equals the sum of all the individual “series” resistances.
 In practice this type of circuit isn’t used much in a house. This is because if 240 volts comes into the house, and there are six lights in series, then each light would only be getting one sixth of that voltage i.e. 40 volts. However, this type of circuit is often used for Christmas tree lights e.g. 20 lights at 12 Volts each equals 240 Volts. The problem with this circuit is that if one light blows, then all the others go out also. This is because the wire connection to the next light is broken, so the circuit is not complete.
In practice this type of circuit isn’t used much in a house. This is because if 240 volts comes into the house, and there are six lights in series, then each light would only be getting one sixth of that voltage i.e. 40 volts. However, this type of circuit is often used for Christmas tree lights e.g. 20 lights at 12 Volts each equals 240 Volts. The problem with this circuit is that if one light blows, then all the others go out also. This is because the wire connection to the next light is broken, so the circuit is not complete.
A series circuit is often used with batteries. When batteries are in series, the total voltage equals the sum of all the individual voltages, and the total current flowing through the whole circuit is the same as the current flowing through any one battery. For example: four 1.5 volt 500mA batteries in series with each other makes a battery of 6 volts (4 x 1.5) @500mA.
CONCEPT 2:
Consider this circuit of six light bulbs. Because they are connected across each other, or in parallel with each other, they are said to be connected in parallel.
What happens with the voltage, current and resistance in this type of circuit is in contrast with what happens in a series circuit.
Voltage: The voltage across each light is the same as the “voltage in”. If 220 volts is coming in to the circuit, then there is 220 volts across each individual light.
Current: The current going into the circuit is the sum of the currents in each individual light. If the current through each light is 1 amp, then the total current coming into this circuit would be 6 amps (6 x 1 amp).
Resistance: The total resistance is calculated by a complicated formula that we don’t need to learn at this stage. Suffice to say that the total resistance is less than the lowest individual resistance. Here is the formula for those who really need to know:
 In practice this type of circuit is used in houses. e.g. If you have 220 volts coming into your house, then all the lights and power outlets (power sockets) are also 220 volts because they are connected in parallel.
In practice this type of circuit is used in houses. e.g. If you have 220 volts coming into your house, then all the lights and power outlets (power sockets) are also 220 volts because they are connected in parallel.
Batteries can also be connected in parallel. The output voltage of two batteries in parallel is the same as one of the batteries, but the current capacity is doubled. For Example: two 12 volt 100 amp/hour car batteries in parallel make up the equivalent of a 12 volt 200 amp/hour battery. The same two batteries in series would make the equivalent of a 24 volt 100 amp/hour battery.
Putting it all Together
Some people are excited by the way that the Ohm’s law formula can be substituted into our Power formula to create new formulas. For those of you who like to play with formulas, you can work out how this is done; for the rest, just accept that this table shows the various combinations of these formulas.
This table displays all the possible combinations using the two basic formulas we have learned. Try using a calculator and the following values to check it out:
V = 12 volts I = 2 amps R = 6Ω P = 24 watts
You might like to print the table out and stick it to your multi-meter case or workshop wall for handy future reference.
A simple calculator to do all these combinations is available here.
Congratulations on having finished reading these first two articles about electrical fundamentals.. It has been very heavy with theory and all sorts of formulas, but now you have the basics to understand most electrical and electronic principles.